question
How many distinct binary tree shapes exist for n nodes?
ex. For 3 nodes there are 5 distinct shapes:
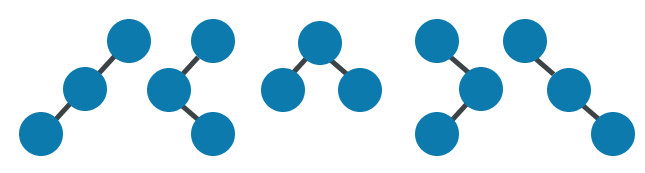
ex. For 3 nodes there are 5 distinct shapes:

Calculate number of tree shapes for small values of n and find a pattern.
count(0) = 1
c(1) = c(0)*c(0) = 1
c(2) = c(0)*c(1) + c(1)*c(0) = 2
c(3) = c(0)*c(2) + c(1)*c(1) + c(2)*c(0) = 5
c(4) = c(0)*c(3) + c(1)*c(2) + c(2)*c(1) + c(3)*c(0) = 14
This can be generalized to: c(n) = c(0)*c(n - 1) + c(1)*c(n - 2) + ... + c(n -1)*c(0)
The pattern is in fact well known as the Catalan numbers and can be rewritten as:
c(n) = (2n)! / (n + 1)!n!
Thoughts or alternate solution? Let us know in the comments below!
c(1) = c(0)*c(0) = 1
c(2) = c(0)*c(1) + c(1)*c(0) = 2
c(3) = c(0)*c(2) + c(1)*c(1) + c(2)*c(0) = 5
c(4) = c(0)*c(3) + c(1)*c(2) + c(2)*c(1) + c(3)*c(0) = 14
This can be generalized to: c(n) = c(0)*c(n - 1) + c(1)*c(n - 2) + ... + c(n -1)*c(0)
The pattern is in fact well known as the Catalan numbers and can be rewritten as:
c(n) = (2n)! / (n + 1)!n!
Thoughts or alternate solution? Let us know in the comments below!